量子化
量子化横分子等高数法の提案。近似を使った量子化の方法。
[1129] 新設計法 量子化横分子等高数法について 投稿者:めぐろ 投稿日:2003/03/28(Fri) 13:31
[1130] 量子化横分子等高数法の応用(1) 投稿者:めぐろ 投稿日:2003/03/28(Fri) 13:40
[1131] 量子化横分子等高数法の応用(2) 投稿者:めぐろ 投稿日:2003/03/28(Fri) 13:45
[1132] 量子化横分子等高数法の応用(3) 投稿者:めぐろ 投稿日:2003/03/28(Fri) 13:50
[1133] 無題 投稿者:めぐろ 投稿日:2003/03/28(Fri) 14:01
[1134] 無題 投稿者:めぐろ 投稿日:2003/03/28(Fri) 14:28
[1135] 折紙設計における誤差の取り扱い 投稿者:めぐろ 投稿日:2003/03/29(Sat) 15:33
[1136] 角二等辺三角形分子の量子化 投稿者:めぐろ 投稿日:2003/03/29(Sat) 16:08
[1138] 実用できそうな直角二等辺三角形分子の量子化 投稿者:めぐろ 投稿日:2003/03/29(Sat) 16:43
[1140] ツルの量子化 投稿者:めぐろ 投稿日:2003/03/29(Sat) 18:54
[1141] 誤差 投稿者:めぐろ 投稿日:2003/03/29(Sat) 19:45
[1144] 22.5°系量子化 投稿者:タト 投稿日:2003/03/29(Sat) 23:54
[1146] 量子化といえば 投稿者:めぐろ 投稿日:2003/03/30(Sun) 12:02
[1147] タトさん 投稿者:めぐろ 投稿日:2003/03/30(Sun) 12:57
[1148] a:0:c_(d:e)の折線パターンはa':0:c'_(d:e)...a'+c'>=a+c でも同様に折れること 投稿者:めぐろ 投稿日:2003/03/30(Sun) 13:07
[1152] なんちゃってピタゴラス三角形の量子化 投稿者:めぐろ 投稿日:2003/03/30(Sun) 21:0
[1153] なんちゃってピタゴラスの三角形の種類 投稿者:めぐろ 投稿日:2003/03/30(Sun) 22:14
[1154] [1153] の訂正 投稿者:めぐろ 投稿日:2003/03/30(Sun) 22:25
[1155] 続なんちゃってピタゴラスの三角形の種類 投稿者:めぐろ 投稿日:2003/03/30(Sun) 22:41
[1156] 続続なんちゃってピタゴラスの三角形 投稿者:めぐろ 投稿日:2003/03/30(Sun) 22:57
[1157] 30度-60度-90度の直角三角形の量子化 投稿者:めぐろ 投稿日:2003/03/30(Sun) 23:38
BACK TO INDEX
ようこそ、折紙のホームページへ
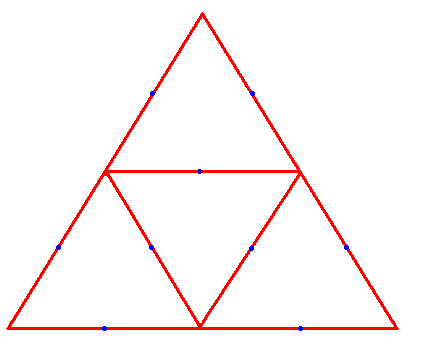 この図は折り畳み可能です。
この図は折り畳み可能です。
 この図は折り畳み可能です。
この図は折り畳み可能です。
 この図も折り畳み可能です。
この図も折り畳み可能です。
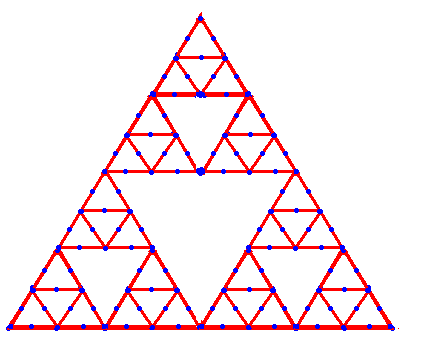 この図も折り畳み可です(以下無限に続く)。
この図も折り畳み可です(以下無限に続く)。
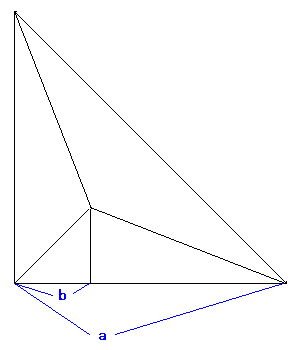 左図のように直角二等辺三角形分子の a:b は 2+ルート2:1 なので、辺長の量子化ができなそうですが、設計上の技法で多少の誤差はぜんぜんOKですので、そういう意味からは、いくらでも量子化できます。
左図のように直角二等辺三角形分子の a:b は 2+ルート2:1 なので、辺長の量子化ができなそうですが、設計上の技法で多少の誤差はぜんぜんOKですので、そういう意味からは、いくらでも量子化できます。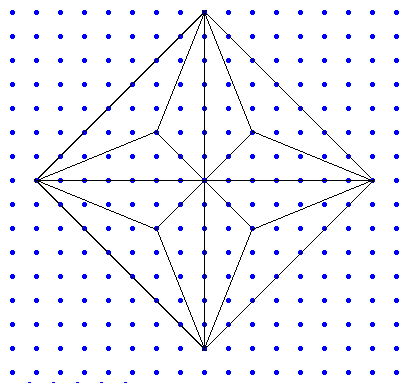 [1137]の直角二等辺三角形分子を、a:b を 7:2 として量子化したものを使って作ったツルです。
[1137]の直角二等辺三角形分子を、a:b を 7:2 として量子化したものを使って作ったツルです。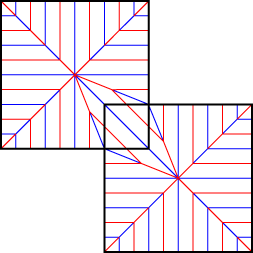 >誤差をつぶすとしたら、それが局所的に限定された折線だけでできること(これは、誤差をつぶすそうとしたらつぶせる方法があるというだけの話で、実際に折る場合は当然誤差なんかいちいちつぶすしたりは普通しない。面倒だし、、、)。
>誤差をつぶすとしたら、それが局所的に限定された折線だけでできること(これは、誤差をつぶすそうとしたらつぶせる方法があるというだけの話で、実際に折る場合は当然誤差なんかいちいちつぶすしたりは普通しない。面倒だし、、、)。
***** 量子化横分子等高数法のあらまし *****
複数の多角形を考える。ここで全ての多角形に対して共通の単位長さtを考える。それぞれの多角形においては、全ての辺の長さが、tの整数倍になっており、その全外周上に矛盾なく等高数が定義できるようになっているものとする。このとき、各多角形を横分子として、隙間なく平面上に敷き詰めたものは折り畳み可能である。このことを利用して折紙設計を行なう。
************************************************
要するに「用紙を長さが整数の線分で適当に分割して、それに等高数が矛盾なく付けば、折り畳みできます。」ということです。
すでにお気づきかとは思いますが、「横分子蛇腹法」は「量子化横分子等高数法」に完全に含まれます。