蛇腹におけるカド領域の効率的パッキング
「神谷パターン」研究・その1
[1047] クモ6 投稿者:めぐろ 投稿日:2003/03/20(Thu) 02:51
[1048] ピタゴラス数 投稿者:めぐろ 投稿日:2003/03/20(Thu) 03:33
[1053] 無題 投稿者:タト 投稿日:2003/03/20(Thu) 12:20
[1054] A2さん 投稿者:めぐろ 投稿日:2003/03/21(Fri) 00:08
[1056] タトさん 投稿者:めぐろ 投稿日:2003/03/21(Fri) 01:36
[1057] 蛇腹におけるカド領域の効率的パッキング(1) 投稿者:めぐろ 投稿日:2003/03/21(Fri) 15:04
[1058] 蛇腹におけるカド領域の効率的パッキング(2) 投稿者:めぐろ 投稿日:2003/03/21(Fri) 15:25
[1059] 蛇腹におけるカド領域の効率的パッキング(3) 投稿者:めぐろ 投稿日:2003/03/21(Fri) 15:37
[1060] 蛇腹におけるカド領域の効率的パッキング(4) 投稿者:めぐろ 投稿日:2003/03/21(Fri) 15:55
[1061] 蛇腹におけるカド領域の効率的パッキング(5) 投稿者:めぐろ 投稿日:2003/03/21(Fri) 16:12
[1062] 蛇腹におけるカド領域の効率的パッキング(6) 投稿者:めぐろ 投稿日:2003/03/21(Fri) 16:27
[1063] 蛇腹におけるカド領域の効率的パッキング(7) 投稿者:めぐろ 投稿日:2003/03/21(Fri) 17:04
[1065] あと 投稿者:タト 投稿日:2003/03/21(Fri) 19:50
[1066] タトさん 投稿者:めぐろ 投稿日:2003/03/21(Fri) 20:06
[1067] 蛇腹におけるカド領域の効率的パッキング(8) 投稿者:めぐろ 投稿日:2003/03/22(Sat) 01:54
[1068] 蛇腹におけるカド領域の効率的パッキング(9) 投稿者:めぐろ 投稿日:2003/03/22(Sat) 02:13
[1069] 蛇腹におけるカド領域の効率的パッキング(10) 投稿者:めぐろ 投稿日:2003/03/22(Sat) 03:09
[1070] 蛇腹におけるカド領域の効率的パッキング(11) 投稿者:めぐろ 投稿日:2003/03/22(Sat) 03:36
[1071] 蛇腹におけるカド領域の効率的パッキング(12) 投稿者:めぐろ 投稿日:2003/03/22(Sat) 04:03
[1072] 蛇腹におけるカド領域の効率的パッキング(13) 投稿者:めぐろ 投稿日:2003/03/22(Sat) 04:07
[1073] 蛇腹におけるカド領域の効率的パッキング(14) 投稿者:めぐろ 投稿日:2003/03/22(Sat) 04:13
[1074] 蛇腹におけるカド領域の効率的パッキング(15) 投稿者:めぐろ 投稿日:2003/03/22(Sat) 05:54
[1091] 8-1-8系 投稿者:めぐろ 投稿日:2003/03/23(Sun) 15:30
[1092] 蛇腹方形領域の重なりの表し方 投稿者:めぐろ 投稿日:2003/03/23(Sun) 17:12
[1093] 蛇腹方形領域の重なりが可能かどうかの判定式 投稿者:めぐろ 投稿日:2003/03/23(Sun) 17:54
[1094] 蛇腹方形領域の判定式 投稿者:めぐろ 投稿日:2003/03/23(Sun) 17:55
[1102] 5:0:5_(1:3) の折り方 投稿者:めぐろ 投稿日:2003/03/25(Tue) 01:19
[1108] 蛇腹の等高数に関する法則(1) 投稿者:めぐろ 投稿日:2003/03/25(Tue) 18:20
[1109] 蛇腹の等高数に関する法則(2) 投稿者:めぐろ 投稿日:2003/03/25(Tue) 18:28
[1110] 蛇腹の等高数に関する法則(3) 投稿者:めぐろ 投稿日:2003/03/25(Tue) 18:34
[1111] a:b:c_(d:e) で表せる蛇腹方形領域の重なりが可能となるための条件のまとめ 投稿者:めぐろ 投稿日:2003/03/25(Tue) 18:47
[1112] 続 5:0:5_(1:3) の折り方 投稿者:めぐろ 投稿日:2003/03/25(Tue) 21:29
[1113] 続続 5:0:5_(1:3) の折り方 投稿者:めぐろ 投稿日:2003/03/25(Tue) 21:35
[1114] やっと消化したと思ったらまた大量投稿が… 投稿者:S太郎 投稿日:2003/03/26(Wed) 12:54
[1116] S太郎さん 投稿者:めぐろ 投稿日:2003/03/26(Wed) 20:12
[1117] 拡張蛇腹と等高数 投稿者:めぐろ 投稿日:2003/03/26(Wed) 20:59
[1118] すごいですね… 投稿者:タト 投稿日:2003/03/26(Wed) 22:16
[1120] タトさん 投稿者:めぐろ 投稿日:2003/03/27(Thu) 16:02
[1121] 唐揚げにソースかけてる奴、どうかしてるよ 投稿者:S太郎 投稿日:2003/03/27(Thu) 16:41
[1125] 無題 投稿者:タト 投稿日:2003/03/27(Thu) 17:43
[1126] S太郎さん 投稿者:めぐろ 投稿日:2003/03/27(Thu) 17:57
[1127] タトさん 投稿者:めぐろ 投稿日:2003/03/27(Thu) 18:19
[1214] >目黒様:連絡 投稿者:神谷哲史 投稿日:2003/04/16(Wed) 20:52
[1216] 神谷さん 投稿者:めぐろ 投稿日:2003/04/17(Thu) 01:23
[1217] 仮称 投稿者:S太郎 投稿日:2003/04/17(Thu) 22:56
[1218] もちろん 投稿者:S太郎 投稿日:2003/04/18(Fri) 12:29
[1219] 仮称 投稿者:めぐろ 投稿日:2003/04/19(Sat) 01:05
[1231] 仮称 投稿者:小松英夫 投稿日:2003/04/22(Tue) 01:34
[1233] 仮称 投稿者:めぐろ 投稿日:2003/04/22(Tue) 23:41
[1243] 神谷パターン…… 投稿者:神谷哲史 投稿日:2003/04/24(Thu) 20:02
[1248] 神谷パターン 投稿者:めぐろ 投稿日:2003/04/25(Fri) 14:19
BACK TO INDEX
ようこそ、折紙のホームページへ
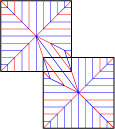
 まずは左図のような、長さ5のカドの領域について見てみます。
まずは左図のような、長さ5のカドの領域について見てみます。 まずは左図のような、長さ5のカドの領域について見てみます。
まずは左図のような、長さ5のカドの領域について見てみます。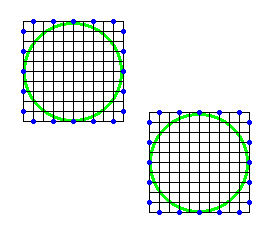 では、左図の2つの方形領域を蛇腹として整合性を持たせつつ
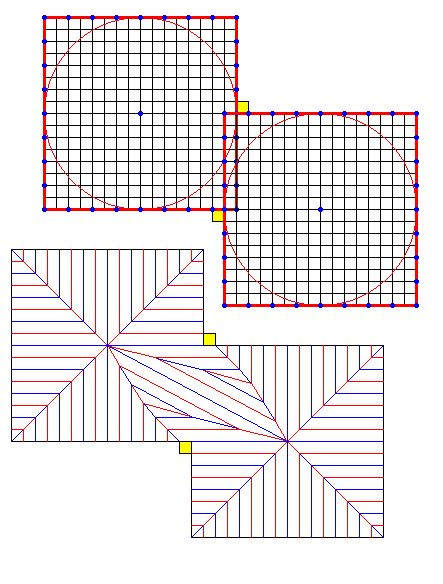
では、左図の2つの方形領域を蛇腹として整合性を持たせつつ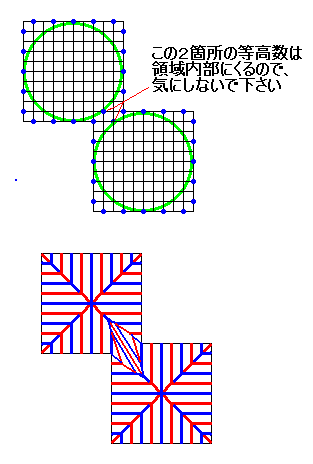 また、別のパターンを考えてみますと、左図のようなパッキングも[1059]の2条件を満たしますから、可能です。
また、別のパターンを考えてみますと、左図のようなパッキングも[1059]の2条件を満たしますから、可能です。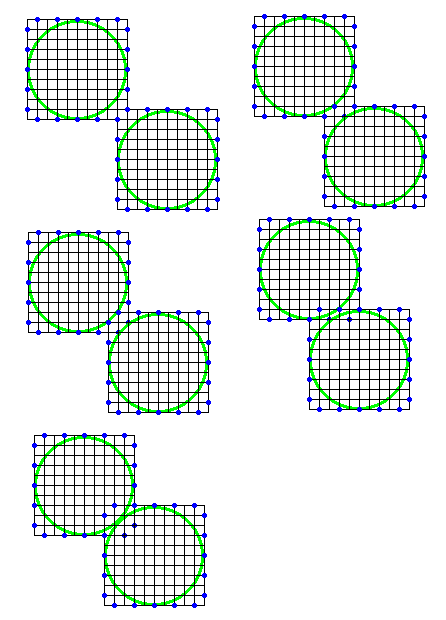 これまでのことから、2つの方形領域(ともに長さ5のカドに対応)を蛇腹として整合性を持たせつつ効率よくパッキングさせるには左図のようなパターンがあることが分かりました(これらのパターンは非ピタゴラス的です)。
これまでのことから、2つの方形領域(ともに長さ5のカドに対応)を蛇腹として整合性を持たせつつ効率よくパッキングさせるには左図のようなパターンがあることが分かりました(これらのパターンは非ピタゴラス的です)。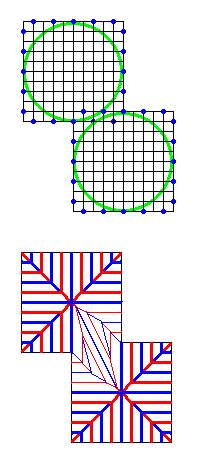 [1062] の図右下のパターンの折り方を示しておきます。
[1062] の図右下のパターンの折り方を示しておきます。
 2x4だけ重なるこんなパターンもありますよね。
2x4だけ重なるこんなパターンもありますよね。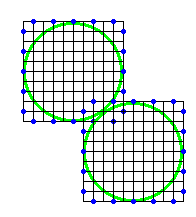 ほんとだ!このパターンですね。
ほんとだ!このパターンですね。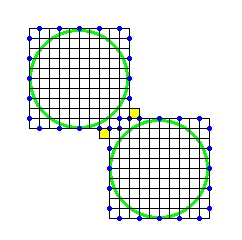 2つの方形領域(ともに長さ5のカドに対応)の間に幅1の帯領域がある場合について考えてみます。
2つの方形領域(ともに長さ5のカドに対応)の間に幅1の帯領域がある場合について考えてみます。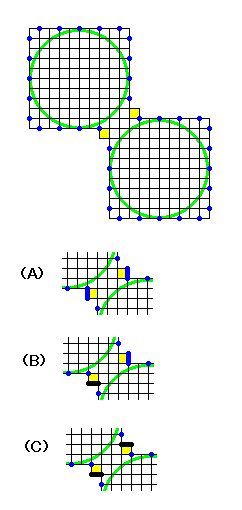 帯領域の表しかたが定まったら、次は等高数を矛盾なくすることについて考えましょう。
帯領域の表しかたが定まったら、次は等高数を矛盾なくすることについて考えましょう。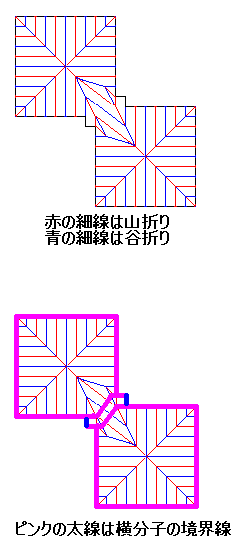 [1068] では矛盾のない等高数のつけ方として3通りが可能であると書きましたが、実際はどれかひとつの折り方ができると、残りの2通りに簡単に変換できることがほとんどですので、特に、問題がない場合は、(A)タイプの表し方(等高数0の太線を2本描くタイプ)をするようにします。
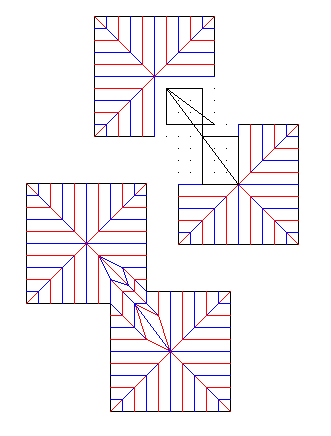
[1068] では矛盾のない等高数のつけ方として3通りが可能であると書きましたが、実際はどれかひとつの折り方ができると、残りの2通りに簡単に変換できることがほとんどですので、特に、問題がない場合は、(A)タイプの表し方(等高数0の太線を2本描くタイプ)をするようにします。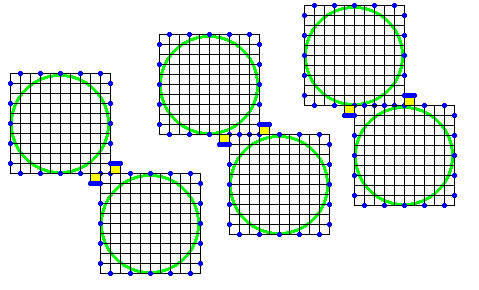 可能なパターンをシラミつぶしてみる(その1)。
可能なパターンをシラミつぶしてみる(その1)。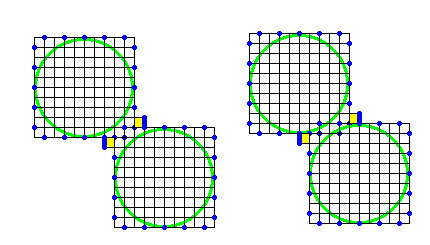 可能なパターンをシラミつぶしてみる(その2)。
可能なパターンをシラミつぶしてみる(その2)。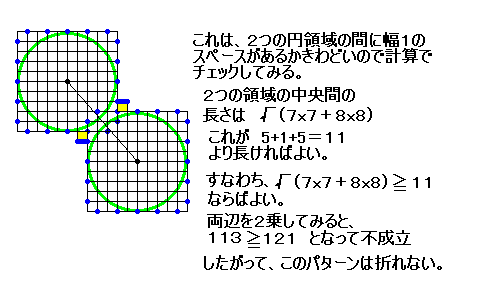 ちなみに、ここの左図のようなパターンは、領域の干渉が避けられないため、折れません。
ちなみに、ここの左図のようなパターンは、領域の干渉が避けられないため、折れません。
 さらに5:0:5_(1:3) の別の折り方です。これもピタゴラス三角形を4つ使っていますが、少しわかりにくいので、図の左上にその4つのピタゴラス三角形を黒線で描いておきます。
さらに5:0:5_(1:3) の別の折り方です。これもピタゴラス三角形を4つ使っていますが、少しわかりにくいので、図の左上にその4つのピタゴラス三角形を黒線で描いておきます。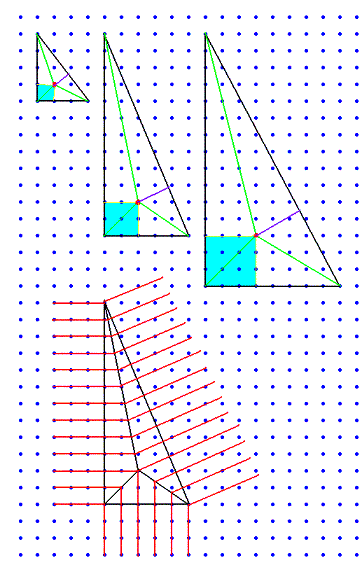 すげーなぁ(そればっかだ)
すげーなぁ(そればっかだ)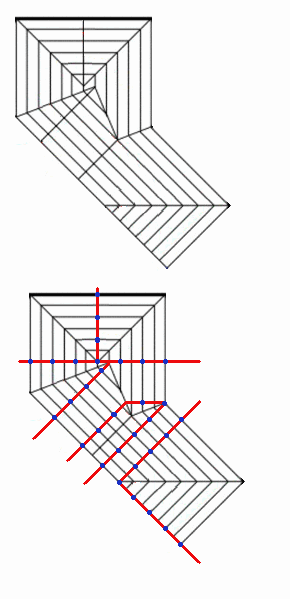 左図はS太郎さんのクモ5の拡張蛇腹の部分を使わせていただいています。
左図はS太郎さんのクモ5の拡張蛇腹の部分を使わせていただいています。 3:4:5蛇腹のとき「折りたたみ可能な条件」という観点から考えたとき重要になるポイントになる気がしました。
3:4:5蛇腹のとき「折りたたみ可能な条件」という観点から考えたとき重要になるポイントになる気がしました。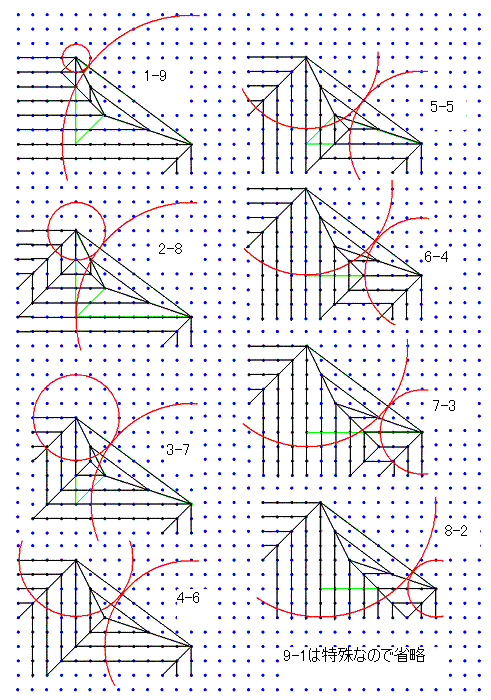 私は、神谷パターンは蛇腹系で方形領域が重なるときに、「カド頂点を直線で結ぶという円領域分子法の基本操作」を使ったのち、拡張蛇腹で整合性を出した形、と捉えています。そのうえで、[1113]のような形は、等高数を鑑みつつ斜線の蛇腹をずらして結合した形とも解釈できそうですね。
私は、神谷パターンは蛇腹系で方形領域が重なるときに、「カド頂点を直線で結ぶという円領域分子法の基本操作」を使ったのち、拡張蛇腹で整合性を出した形、と捉えています。そのうえで、[1113]のような形は、等高数を鑑みつつ斜線の蛇腹をずらして結合した形とも解釈できそうですね。
ところで、領域が干渉しているのにちゃんと折れるか不安に感じる人もいるかもしれないが、干渉しているのはカドの領域として方形領域をとっているからであって、カドの領域を円領域に取り直せば干渉はしていないので、工夫すれば折ることは可能なのである。このような工夫は神谷氏によって進められ、ピタゴラス数を使ったいわば神谷パターンなるものが知られている。今回の場合もできるなら神谷パターンを使いたいのだが、とりあえず、速やかに折れるパターンを手にいれるという目的では、ユニバーサル分子的な処理で左図の下側をまとめればよい。