重なり可能パターンのしらみつぶし
「神谷パターン」研究・その2
[1091] 8-1-8系 投稿者:めぐろ 投稿日:2003/03/23(Sun) 15:30
[1092] 蛇腹方形領域の重なりの表し方 投稿者:めぐろ 投稿日:2003/03/23(Sun) 17:12
[1093] 蛇腹方形領域の重なりが可能かどうかの判定式 投稿者:めぐろ 投稿日:2003/03/23(Sun) 17:54
[1094] 蛇腹方形領域の判定式 投稿者:めぐろ 投稿日:2003/03/23(Sun) 17:55
[1095] 重なり可能パターンのしらみつぶし(1) 投稿者:めぐろ 投稿日:2003/03/23(Sun) 19:05
[1096] 重なり可能パターンのしらみつぶし(2) 投稿者:めぐろ 投稿日:2003/03/23(Sun) 19:19
[1097] 重なり可能パターンのしらみつぶし(3) 投稿者:めぐろ 投稿日:2003/03/23(Sun) 19:33
[1098] 重なり可能パターンのしらみつぶし(4) 投稿者:めぐろ 投稿日:2003/03/23(Sun) 19:39
[1100] 重なり可能パターンのしらみつぶし(5) 投稿者:めぐろ 投稿日:2003/03/23(Sun) 21:19
[1101] 重なり可能パターンのしらみつぶし(6) 投稿者:めぐろ 投稿日:2003/03/23(Sun) 21:49
[1122] 重なり可能パターンのしらみつぶし(7) 投稿者:めぐろ 投稿日:2003/03/27(Thu) 16:45
[1123] 重なり可能パターンのしらみつぶし(8) 投稿者:めぐろ 投稿日:2003/03/27(Thu) 17:24
[1124] 重なり可能パターンのしらみつぶし(9) 投稿者:めぐろ 投稿日:2003/03/27(Thu) 17:27
[1128] 重なり可能パターンのしらみつぶし(10) 投稿者:めぐろ 投稿日:2003/03/27(Thu) 22:34
[1139] 重なり可能パターンのしらみつぶし(11) 投稿者:めぐろ 投稿日:2003/03/29(Sat) 17:07
[1148] a:0:c_(d:e)の折線パターンはa':0:c'_(d:e)...a'+c'>=a+c でも同様に折れること 投稿者:めぐろ 投稿日:2003/03/30(Sun) 13:07
[1150] 重なり可能パターンのしらみつぶし(11) 投稿者:めぐろ 投稿日:2003/03/30(Sun) 18:14
[1151] 重なり可能パターンのしらみつぶし(12) 投稿者:めぐろ 投稿日:2003/03/30(Sun) 18:24
[1158] 重なり可能パターンのしらみつぶし(12) 投稿者:めぐろ 投稿日:2003/03/31(Mon) 01:15
[1159] 重なり可能パターンのしらみつぶし(13) 投稿者:めぐろ 投稿日:2003/03/31(Mon) 01:29
[1160] 重なり可能パターンのしらみつぶし(14) 投稿者:めぐろ 投稿日:2003/03/31(Mon) 01:48
[1161] 重なり可能パターンのしらみつぶし(15) 投稿者:めぐろ 投稿日:2003/03/31(Mon) 02:27
[1162] 重なり可能パターンのしらみつぶし(16) 投稿者:めぐろ 投稿日:2003/03/31(Mon) 20:57
[1163] 重なり可能パターンのしらみつぶし(17) 投稿者:めぐろ 投稿日:2003/03/31(Mon) 22:06
[1164] 重なり可能パターンのしらみつぶし(18) 投稿者:めぐろ 投稿日:2003/03/31(Mon) 22:17
[1166] 重なり可能パターンのしらみつぶし(19) 投稿者:めぐろ 投稿日:2003/03/31(Mon) 22:54
[1167] 重なり可能パターンのしらみつぶし(20) 投稿者:めぐろ 投稿日:2003/03/31(Mon) 23:20
[1168] 重なり可能パターンのしらみつぶし(21) 投稿者:めぐろ 投稿日:2003/03/31(Mon) 23:46
[1169] 重なり可能パターンのしらみつぶし(22) 投稿者:めぐろ 投稿日:2003/04/01(Tue) 00:12
[1171] 重なり可能パターンのしらみつぶし(23) 投稿者:めぐろ 投稿日:2003/04/01(Tue) 00:36
[1172] 重なり可能パターンのしらみつぶし(24) 投稿者:めぐろ 投稿日:2003/04/01(Tue) 01:26
[1173] 重なり可能パターンのしらみつぶし(25) 投稿者:めぐろ 投稿日:2003/04/01(Tue) 02:12
[1174] 重なり可能パターンのしらみつぶし(26) 投稿者:めぐろ 投稿日:2003/04/02(Wed) 10:21
[1175] 重なり可能パターンのしらみつぶし(27) 投稿者:めぐろ 投稿日:2003/04/02(Wed) 10:26
[1176] 重なり可能パターンのしらみつぶし(28) 投稿者:めぐろ 投稿日:2003/04/03(Thu) 10:49
[1177] 重なり可能パターンのしらみつぶし(28) 投稿者:めぐろ 投稿日:2003/04/03(Thu) 10:51
[1178] 重なり可能パターンのしらみつぶし(29) 投稿者:めぐろ 投稿日:2003/04/03(Thu) 21:52
[1179] 重なり可能パターンのしらみつぶし(30) 投稿者:めぐろ 投稿日:2003/04/05(Sat) 00:01
[1180] 重なり可能パターンのしらみつぶし(31) 投稿者:めぐろ 投稿日:2003/04/05(Sat) 00:03
[1181] 重なり可能パターンのしらみつぶし(32) 投稿者:めぐろ 投稿日:2003/04/05(Sat) 00:40
[1182] 重なり可能パターンのしらみつぶし(33) 投稿者:めぐろ 投稿日:2003/04/05(Sat) 01:00
[1183] 重なり可能パターンのしらみつぶし(34) 投稿者:めぐろ 投稿日:2003/04/05(Sat) 01:15
[1184] 重なり可能パターンのしらみつぶし(35) 投稿者:めぐろ 投稿日:2003/04/05(Sat) 01:47
[1185] 重なり可能パターンのしらみつぶし(36) 投稿者:めぐろ 投稿日:2003/04/05(Sat) 01:59
[1186] 重なり可能パターンのしらみつぶし(37) 投稿者:めぐろ 投稿日:2003/04/05(Sat) 10:07
[1187] 重なり可能パターンのしらみつぶし(38) 投稿者:めぐろ 投稿日:2003/04/06(Sun) 03:27
[1188] 重なり可能パターンのしらみつぶし(39) 投稿者:めぐろ 投稿日:2003/04/06(Sun) 04:15
[1189] 重なり可能パターンのしらみつぶし(40) 投稿者:めぐろ 投稿日:2003/04/06(Sun) 22:59
BACK TO INDEX
ようこそ、折紙のホームページへ
 蛇腹方形領域の重なり判定式を使って、Excelでしらみつぶしをかけます。まずは 5:0:5_(d:e)系についてです。
蛇腹方形領域の重なり判定式を使って、Excelでしらみつぶしをかけます。まずは 5:0:5_(d:e)系についてです。 蛇腹方形領域の重なり判定式を使って、Excelでしらみつぶしをかけます。まずは 5:0:5_(d:e)系についてです。
蛇腹方形領域の重なり判定式を使って、Excelでしらみつぶしをかけます。まずは 5:0:5_(d:e)系についてです。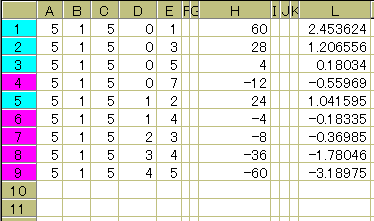 ついで、5:1:5_(d:e)系についてです。
ついで、5:1:5_(d:e)系についてです。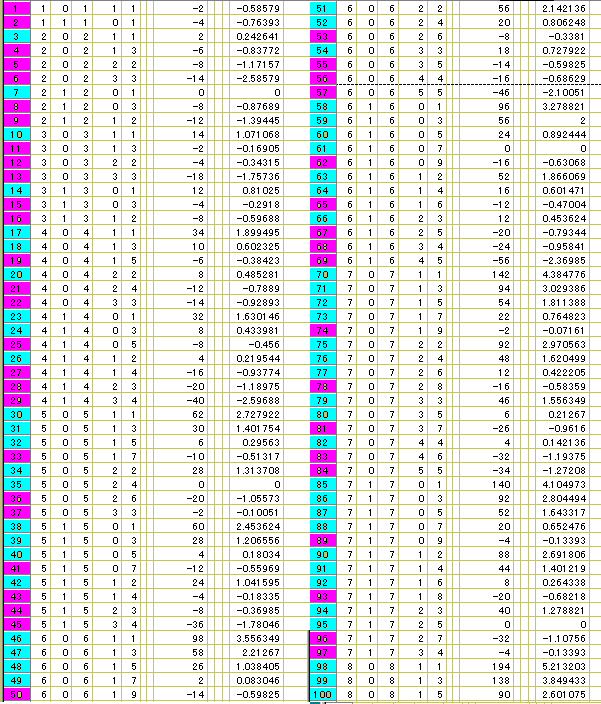
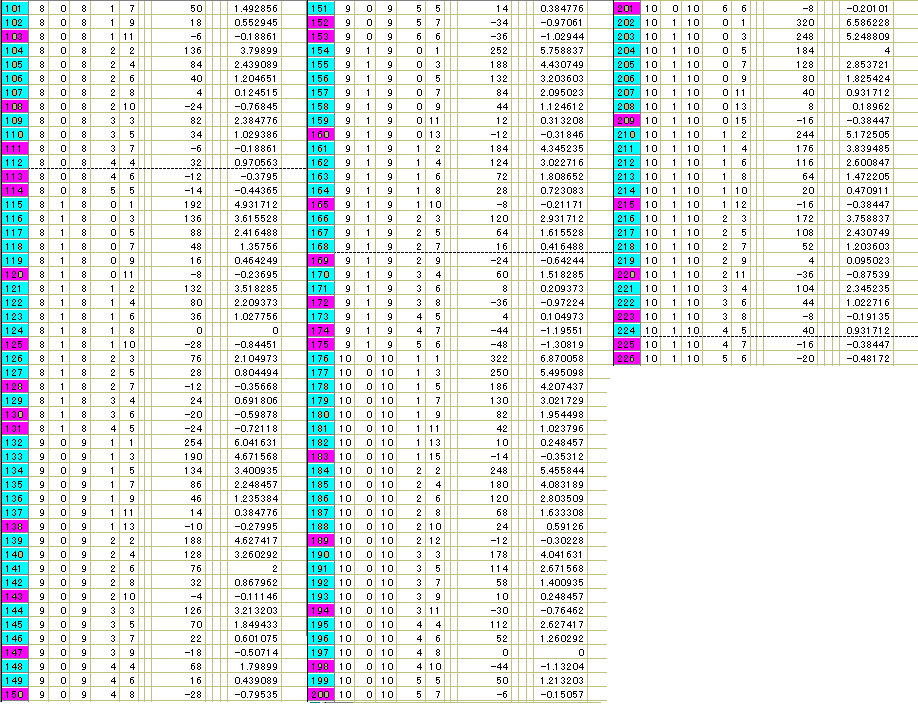
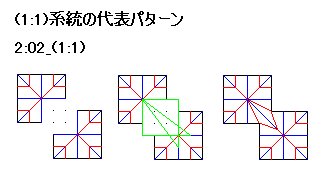 取りあえず1系統
取りあえず1系統
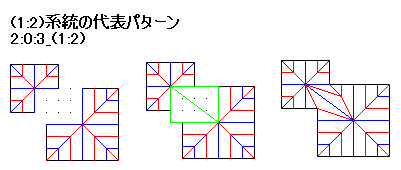 もう1系統
もう1系統
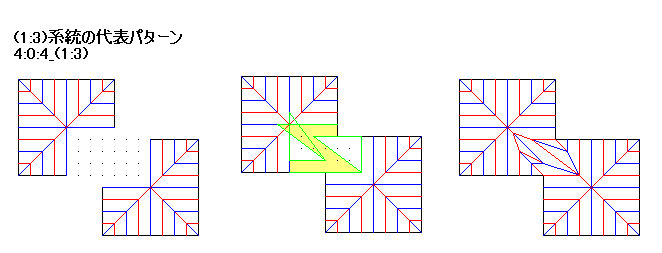 この系統は折り方に工夫がいる。
この系統は折り方に工夫がいる。
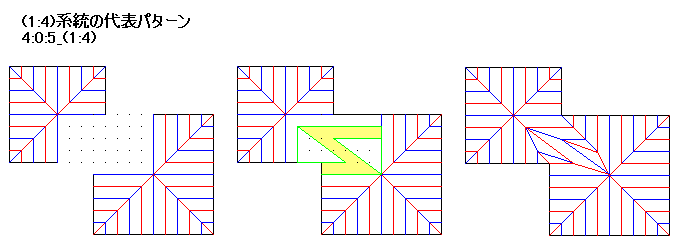 ピタゴラス三角形の間にZ字型の帯をはさむ技法も神谷さん由来。これが決まると折っていて気持ちが良い。
ピタゴラス三角形の間にZ字型の帯をはさむ技法も神谷さん由来。これが決まると折っていて気持ちが良い。
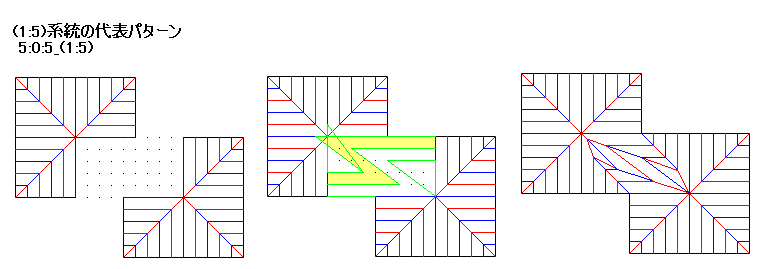
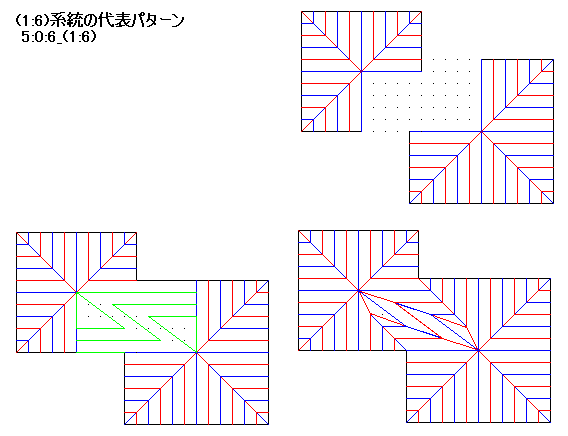
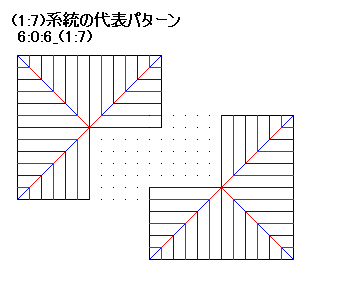 6:0:6_(1:7)系統を厳密に正確に折るには、ユニバーサルモレキュールを用いる方法がありますが、結構手間がかかります。
6:0:6_(1:7)系統を厳密に正確に折るには、ユニバーサルモレキュールを用いる方法がありますが、結構手間がかかります。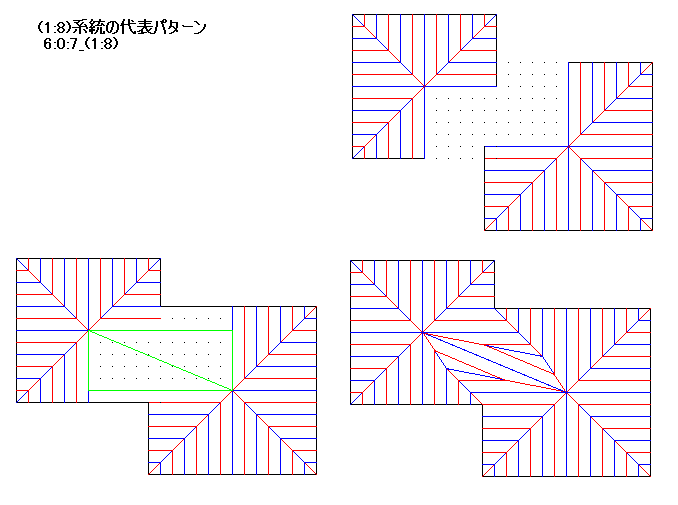 6:0:7_(1:8)系統は、3辺の比が5:12:13のピタゴラスの三角形を用いて、厳密かつ簡単に折れます。
6:0:7_(1:8)系統は、3辺の比が5:12:13のピタゴラスの三角形を用いて、厳密かつ簡単に折れます。
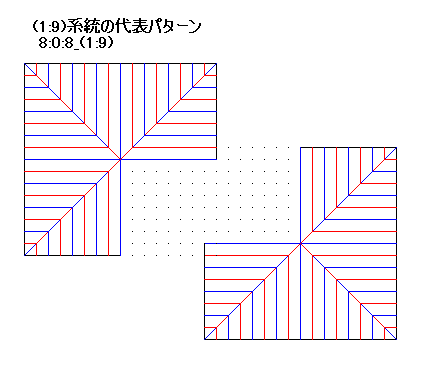 8:0:8_(1:9)も、厳密に正確に折るには、ユニバーサルモレキュールを用いる方法がありますが、結構手間がかかります。
8:0:8_(1:9)も、厳密に正確に折るには、ユニバーサルモレキュールを用いる方法がありますが、結構手間がかかります。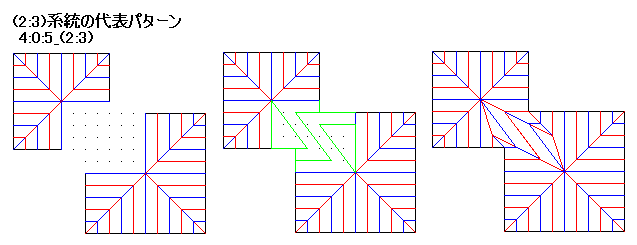 4:0:5_(2:3)
4:0:5_(2:3)
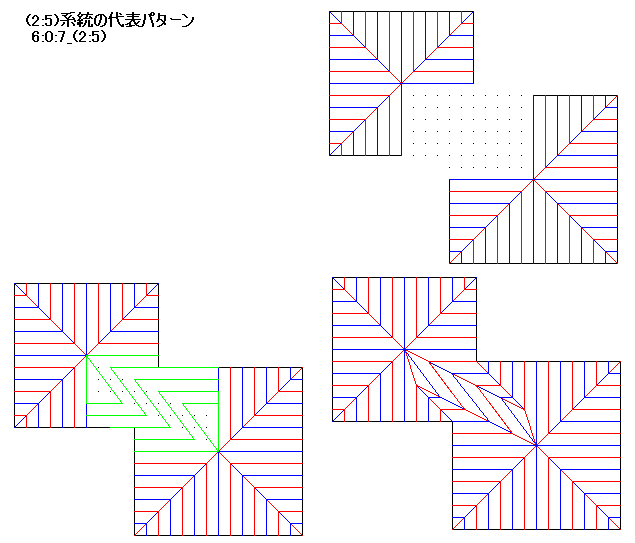 6:0:7_(2:5)
6:0:7_(2:5)
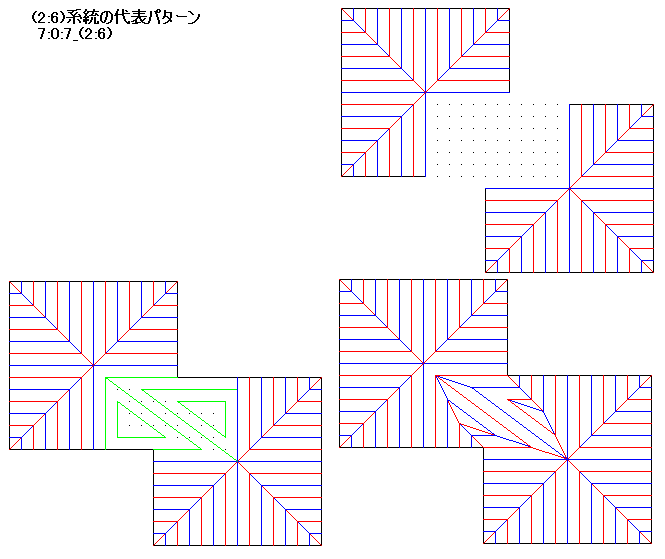 7:0:7_(2:6)
7:0:7_(2:6)
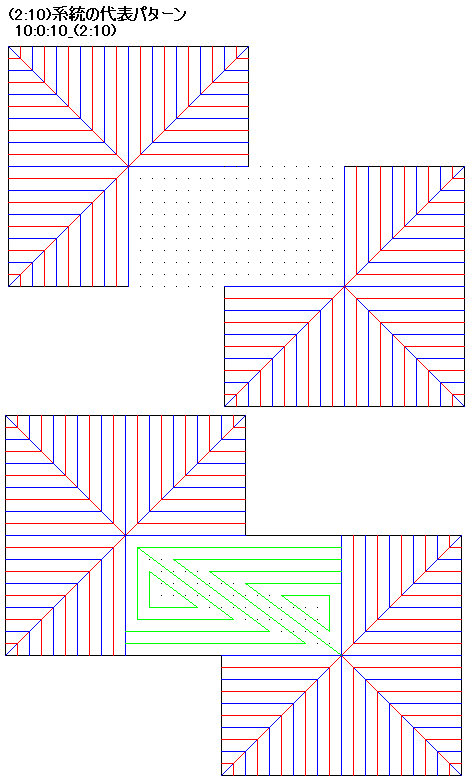 10:010_(2:10)は、5:0:5_(1:5)を2倍に拡大して沈め折りを加えてもできるが、その方法よりこの左図に示した方が簡明。実際の折線パターンは[1174] から類推してください。
10:010_(2:10)は、5:0:5_(1:5)を2倍に拡大して沈め折りを加えてもできるが、その方法よりこの左図に示した方が簡明。実際の折線パターンは[1174] から類推してください。
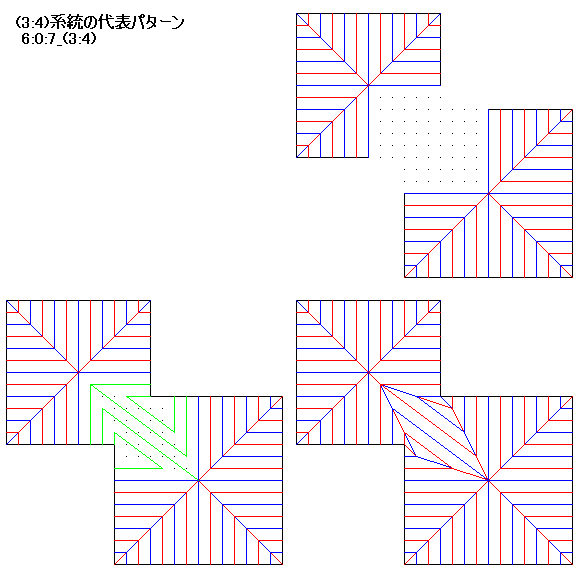 6:0:7_(3:4)
6:0:7_(3:4)
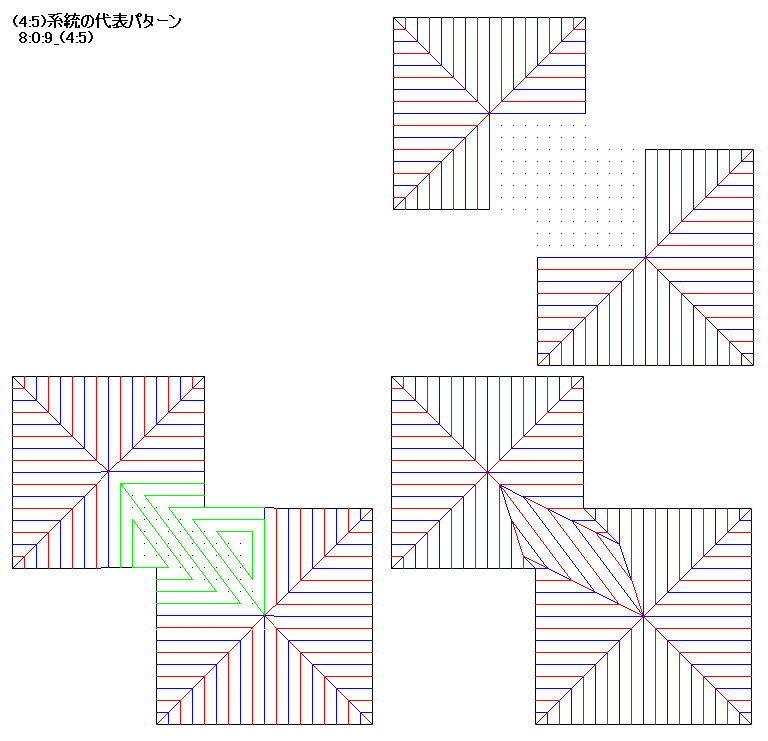 8:0:9_(4:5)
8:0:9_(4:5)
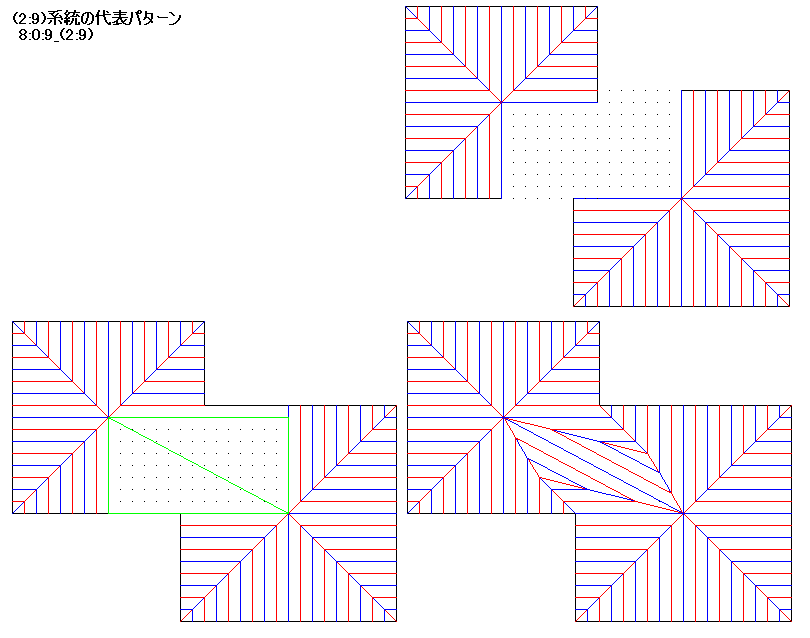 8:0:9_(2:9)には三辺の比が8:15:17のピタゴラス三角形がぴったり
8:0:9_(2:9)には三辺の比が8:15:17のピタゴラス三角形がぴったり
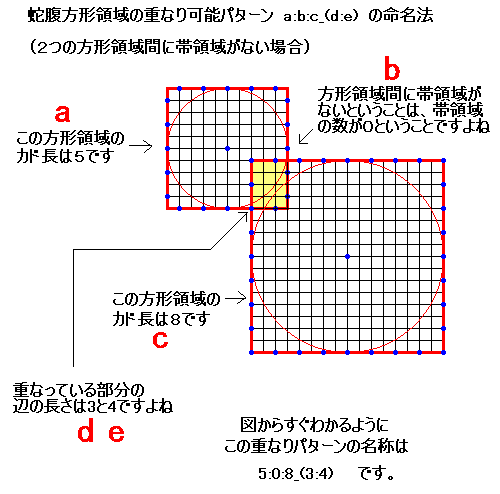 重なりパターンの合理的命名法の 例1 です。
重なりパターンの合理的命名法の 例1 です。
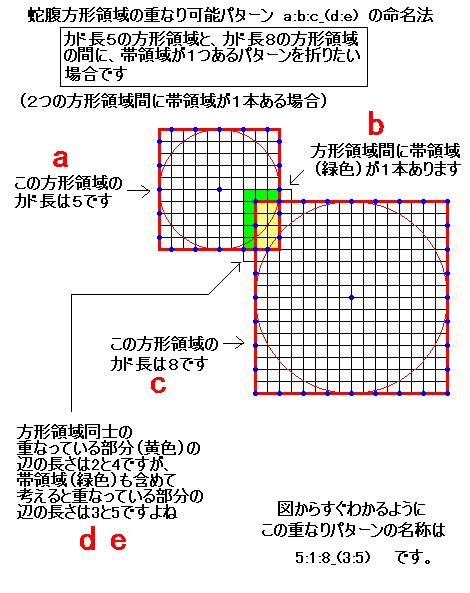 重なりパターンの合理的命名法の 例2 です。
重なりパターンの合理的命名法の 例2 です。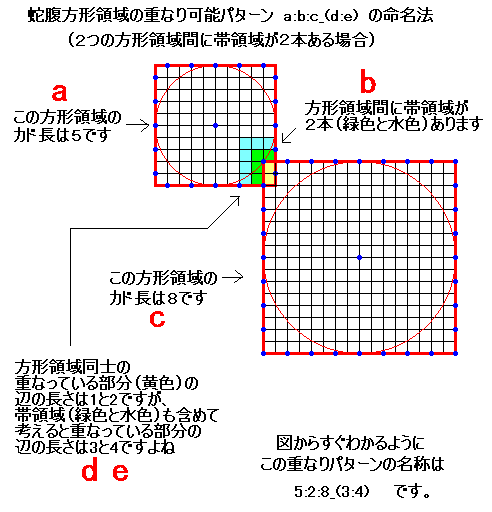 方形領域間に帯領域が複数ある例
方形領域間に帯領域が複数ある例
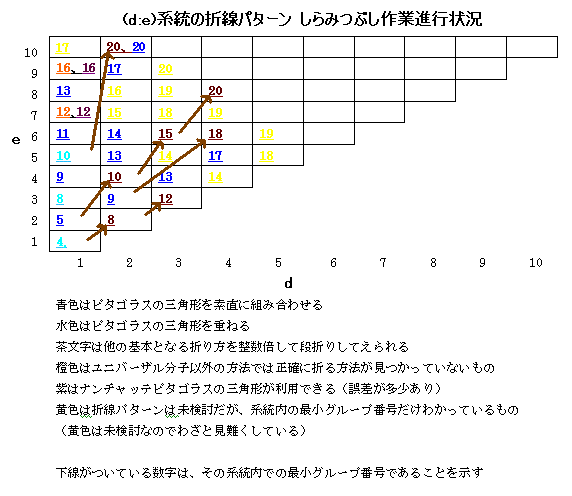 進行状況の表
進行状況の表
 蛇腹における方形領域の重なりパターンをなんちゃってユニバーサル分子を使って折った例
蛇腹における方形領域の重なりパターンをなんちゃってユニバーサル分子を使って折った例
 ユニバーサル分子を用いて、重なりパターンに正確な折線をつけたい場合は、左図のようにします。
ユニバーサル分子を用いて、重なりパターンに正確な折線をつけたい場合は、左図のようにします。
う、、、。